


Mechanics to Metaphor: The Harmonic Series
The Harmonic Series. Back to our plucked string. So far we have been looking at a string vibrating along its entire length and generating a single wave. But there’s another phenomenon that occurs when a string is plucked: in addition to the string vibrating along its entire length, it at the same time vibrates at half its length twice as fast—though to a much lesser degree. To a lesser degree as well, it vibrates at 1/3 its length at 3 times the speed, 1/4 its length at 4 times the speed, and so on.
These “inner vibrations” create smaller waves—harmonics—that travel concurrently with the primary one—the fundamental. We don’t, however, perceive the fundamental and its harmonics as separate pitches. Instead, the harmonics add color to the singular sound of our plucked string: they give it its character. The volume of harmonics in relation to the fundamental, and to each other, let us know that it’s a guitar we’re hearing, and not a banjo or a harp.
 Just which harmonics appear within a sound, and at what amplitude and when, is determined by physics. In the case of our guitar, it’s the length, thickness, material, and tension of the string; the materials of the guitar’s body, which have their own vibratory properties; the fact that the string is stretched across the guitar’s sound hole, which channels some of the waves into the guitar’s interior, where some resonate and get louder while others are absorbed and disappear; and the acoustic properties of the room in which the string is being plucked, where some of the waves are additionally reflected or absorbed. All of this occurs in the instant between the plucking and the hearing, and us identifying the sound as “guitar.”
Just which harmonics appear within a sound, and at what amplitude and when, is determined by physics. In the case of our guitar, it’s the length, thickness, material, and tension of the string; the materials of the guitar’s body, which have their own vibratory properties; the fact that the string is stretched across the guitar’s sound hole, which channels some of the waves into the guitar’s interior, where some resonate and get louder while others are absorbed and disappear; and the acoustic properties of the room in which the string is being plucked, where some of the waves are additionally reflected or absorbed. All of this occurs in the instant between the plucking and the hearing, and us identifying the sound as “guitar.”
The pattern of harmonics, or “partials,” that arises from a fundamental at 2:1, 3:1, 4:1, and so on is called the Harmonic Series. This series doesn’t exist only for a plucked string, of course—it exists in all sound, and in all things that vibrate. As with our guitar string, harmonics everywhere appear how and when depending on the physics of what’s vibrating and where. A trumpet engenders one particular set of harmonics, tires screeching on the pavement, another. Sounds with loud fundamentals and soft harmonics, like a flute, sound “dark” or “pure” to us; sounds with more upper harmonics, like a violin or a sax, sound “bright.” When a sound’s harmonics compete in volume with its fundamental, pitch becomes a bit nebulous—that’s why church bells always sound vaguely out of tune. When harmonics overwhelm the fundamental, or when there are several sources within a sound, or when the source or sources within a sound are shifting shape or moving around, pitch goes out the window—we can’t really hum along with those screeching tires, or a whacked snare drum, or the sound of the surf. Nonetheless, the pattern of harmonics from which all those sounds emerge, the ratios between those harmonics, is always the same.
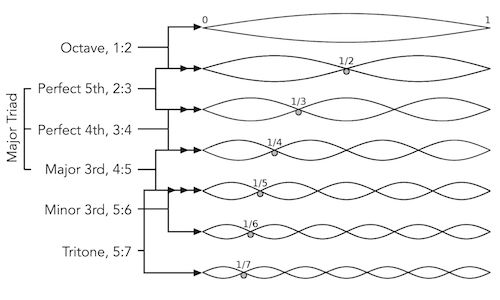
The ratios in the lower reaches of the harmonic series are the basis for harmony in music. 1:1 is a unison, two frequencies the same; frequencies at 2:1 are in an octave relationship; at 2:3, they make a perfect fifth; at 3:4, a perfect fourth; at 4:5 a major third, at 5:6 a minor third. In fact, if we assign each of those first six partials its own note, we get a big fat major chord—easily the most ubiquitous and sonorous harmony in western music. (Most anyone who plays an instrument knows that certain notes go into making one of these chords; fewer realize that each single note within the chord is built, via the Harmonic Series, of the same stuff.) That we find these lower ratio harmonies consonant and pleasing and others less so is more than cultural indoctrination—it is the laws of vibration at work.
Below, the to and fro of a plucked and vibrating string: during the course of one cycle, all of the below (and then some) happens at once. (Keep in mind that middle C, for example, cycles more than 250 times per second.) The frequency shown at the top of the illustration is the fundamental—it would likely sound the loudest, and for us define a pitch. The frequencies below the fundamental are harmonics (or partials, take your pick.) They would sound much softer, and rather than sounding like separate frequencies would instead add color to the sound overall. (If the below illustration was a snapshot of an actual sounded note, the waves would all be at differing heights, depending on their loudness.) The intervals between the harmonics are the basis for harmony in music, as shown at the left of the illustration.
The Seventh Partial and the Harmonic Engine. The relationships between the first six partials of the Harmonic Series are marked by consonance: they are at rest. When the seventh partial arises, however, a dissonance appears between it and the fifth partial below it—a tritone—that sets things in motion, and the Harmonic Engine kicks into gear. What is commonly called “the Circle of Fifths” unfolds, as do diatonic (do-re-mi-fa-so-la-ti) and chromatic (all the notes on the piano) scales. As explained earlier, the Rhythm Line is crossed when frequencies fall; as we’ll see, the Harmonic Engine makes them fall. The Harmonic Engine is explored fully here .
Sonic Archetypes. Along with their role in the Harmonic Engine, the organic harmonies that arise from the first seven partials of the Series play another significant role in Muzoracle mythopoetics: they are the basis of the sonic archetypes that define, along with the suits, the 55 Harmony Cards.